Dear Jayden,
Please click on the worksheet below and download it. Complete the tasks and upload it back to be assessed.
Should you have any question please contact me ay corina@streetvibes.org.
Functional Skills Maths:
Entry 3
Skill Standard:
1
Coverage and Range:
Add and subtract decimals using three-digit numbers.
Understand there are different strategies for adding and subtracting, for example 26 + 19 = 26 + 20 – 1 = 45
Know how to partition numbers, for example 32 + 127 + 6 = 100 + 30 + 20 + 20 + 2 +
7 + 6
Explain the Skill
Addition
You may remember that:
Number order doesn’t matter in addition. This means that 1+ 2 + 3 equals the same as 3 + 2 + 1
Add, plus, sum, altogether, total and increase are all different words that are used in addition. They mean the same. And this means that:
3 add 3 equals 6
3 plus 3 equals 6
The sum of 3 and 3 is 6
3 and 3 altogether make 6 The total of 3 and 3 is 6
Increase 3 by 3 to get 6.
It is likely that every day you use addition to work out small sums in your head. For example, if you were to work out the total price of a chocolate bar and a drink, each costing 50 pence, it is unlikely you would need to write the sum down. Many people will know that 50 p + 50 p = 100 p or £1.
If you are adding together a more complex sum, then it is handy to know several addition methods to make it easier. These are explained on the following pages.
Addition Using Columns
One way of adding numbers together is to write them out in columns of hundreds, tens and units and add each column.
You must make sure that each figure is in the correct column and lined up accurately.
Example
212 + 325
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
H T U
|
Add the units together.
|
e.g. 2 + 5 = 7 units |
|
H T U
Then add the tens together. |
e.g. 1 + 2 = 3 tens |
H T U
Finally, add the hundreds together. e.g. 2 + 3 = 5 hundreds
H T U
Using Columns
Sometimes when you add up the column of hundreds, tens or units there is a carry over into the next column.
You must make sure that each figure is in the correct column and lined up accurately.
Example
476 + 337
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
H T U
4 7 6 + 3 3 7
Add the units together. e.g. 6 + 7 = 13
H T U
4 7 6
+ 3 3 7
Put the 3 in the units column and
3
1 carry the 1 over to the tens column.
Then add the tens together. e.g. 7 + 3 + (the carry over figure, 1) = 11
H T U
4 7 6
+ 3 3 7
Put the 1 in the tens column and 1 3
1 1 carry 1 over to the hundreds column.
Finally, add the hundreds together. e.g. 4 + 3 + (the carry over figure, 1) = 8
H T U
4 7 6
+
8 1 3
1 1
Addition Counting On
You can add numbers together by ‘counting on’.
Examples
2 + 17 Swap the numbers around so the bigger number is first.
17 + 2 Start with 17 then count on 2 numbers, e.g. 18, 19.
Partitioning
Another way of working out an addition sum, the partition method involves you splitting numbers into hundreds, tens and units, and adding them separately, before putting them together for the final answer. For example:
254 + 306
Firstly, separate the hundreds, tens and units…
HTU HTU
256 + 304
Hundreds: 200 + 300
Tens: 50 + 0 Units: 6 + 4
Next, add the individual parts…
200 + 300 = 500
50 + 0 = 50
6 + 4 = 10
Finally, add the different parts together for the answer…
500 + 50 = 550
550 + 10 = 560
So the answer to the sum is:
256 + 304 = 560
– Number Line
Using a number line can help you work out a difficult addition sum. For example:
HTU HTU
144 + 231
First, start at the largest number and partition the small number into hundreds, tens and units.
231 + 100 + 40 + 4
Then, follow each step of the sum along the number line.

- Mental Addition
There are many different methods to use when adding up in your head. Generally, use whatever method you know already. For instance:
Number bonds up to 10. (Pairs of whole numbers that make up 10), for example:
5 + 5 = 10
4 + 6 = 10
3 + 7 = 10
2 + 8 = 10
1 + 9 = 10
Count on in tens and then add the units.
Examples
14 + 36 Using number bonds. 4 + 6 = 10 10 + 30 = 40 40 + 10 = 50
325 + 45 Count on in tens then add the units. 325 + 10 + 10 + 10 + 10 = 365 + 5 = 370
Explain the Skill
Subtraction
You may remember that:
Number order does matter in subtraction. This means that 6 – 4 and 4 – 6 will give completely different answers.
Subtract, reduce, take away, difference, decrease, minus, less than, are all words used in subtraction. They mean the same. And this means that:
Subtract 4 from 6 is 2
Reduce 6 by 4 is 2
6 take away 4 is 2
The difference between 6 and 4 is 2
Decrease 6 by 4 is 2
6 minus 4 is 2
4 is 2 less than 6
Like addition, subtraction is one of the most important mathematical skills you can have.
Again, like addition, it is likely you use subtraction almost every day. Many of the methods you will use are the same, or very similar, to the methods used in addition. These are explained on the following pages.
Subtraction – Partitioning
This method involves you splitting numbers into hundreds, tens and units and subtracting them separately. For example:
225 – 111
First, separate the hundreds, tens and units…
 Hundreds: 200 – 100
Hundreds: 200 – 100
Tens: 20 – 10
Units: 5 – 1
Next, subtract the individual parts…
200 – 100 = 100
20 – 10 = 10
5 – 1 = 4
Finally, add all these answers together.
100 + 10 + 4 = 114
So, the final answer is…
225 – 111 = 114
Subtraction - Using Columns
One way of subtracting numbers is to write them out in columns of hundreds, tens and units and subtract each column in turn.
Make sure that you put the two numbers in the correct order. The number that you are taking away is always placed below the original number and so the bottom number is always taken away from the top number.
You must make sure that each figure is in the correct column and lined up accurately.
Example 1
389 - 164
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
H T U
3 8 9
1 6 4
Subtract the units e.g. 9 - 4 = 5 units
T U
3 8 9
1 6 4
5
Then subtract the tens e.g. 8 - 6 = 2 tens
T U
3 8 9
1 6 4
2 5
Finally, subtract the hundreds e.g. 3 - 1 = 2 hundreds
T U
3 8 9
-
2 2 5
Subtraction - Using Columns
The following examples show different methods of calculating the same sum.
Example 2 Method 1
432 - 54
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
H T U
4 3 2 - 5 4
Subtract the units. If the top number is smaller than the bottom, then you must take 1 ten from the tens column and put it with the 2 to make 12 units.
|
- |
H T U 2 1 3 2 4 |
|
In the units column change 2 to 12 and decrease the top tens figure from 3 to 2
The sum is now 12 – 4 = 8 units |
8
Then subtract the tens. If the top number is smaller than the bottom, then you must take 1 hundred from the hundreds column.
|
-
|
H T U 1 2 3 2 4 7 8 |
|
In the tens column change 2 to 12 and decrease the top tens figure from 4 to 3
The sum is now 12 – 5 = 7 tens |
Finally, subtract the hundreds.
H T U The sum is now 3 – 0 = 3 hundreds
3
4 3 2
-
3 7 8
Subtraction - Using Columns
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
Example 3 Method 2
Set the calculation out in columns. Line up units to units, tens to tens and hundreds to hundreds.
H T U
4 3 2 - 5 4
Subtract the units. If the top number is smaller than the bottom, then you must use 1 ten from the tens column.
|
H T U 1 4 3 2 |
|
In the units column change 2 to 12 and increase the bottom tens figure from 5 to 6
|
5 4 T he sum is now 12 - 4 = 8 units
6 8
Then subtract the tens. If the top number is smaller than the bottom, then you must use 1 hundred from the hundreds column.
|
-
|
H T U 1 1 3 2 4 1 6 7 8 |
|
In the tens column change 3 to 13 and place the 1 underneath the 4 in the hundreds column.
The sum is now 13 - 6 = 7 tens |
Finally, subtract the hundreds.
H T U The sum is now 4 - 1 = 3 hundreds
4 3 2
5 4
1
7 8
Subtraction - Counting On
You can easily work out the answers to take away sums by ‘counting on’ from the smaller given number to the larger number.
Examples
18 − 9
The smaller number is 9 so count on 10, 11, 12, 13, 14, 15, 16, 17, 18.
How many numbers did you count? 10, 11, 12, 13, 14, 15, 16, 17 and 18 = 9 numbers.
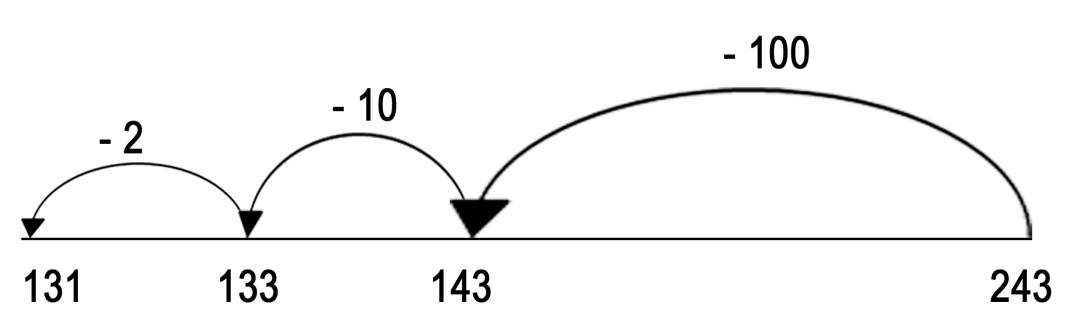
Subtraction – Number Line
Similar to addition, a number line can be used for subtraction. With the subtraction method, you move from right to left, instead of left to right. For example:
243 – 112
First, start with larger number and partition the smaller number into hundreds, tens and units.
243 – 100 – 10 – 2
Then follow each step of the sum along the number line.
Apply the Skill
A customer buys several items from The Music Shop. Their receipt is shown below:
What is the total cost of all three items on the receipt?
£…………
The cost of 20 ukulele lessons is £187. A customer is accidently charged £350. How much should they be refunded?
£…………
A guitar costs the shop £120. They sell it for £209. What is the difference in price?
£…………
You are asked to put up a display in the shop.
The display takes up 150 cm of space. The space for the display is 185 cm. How much space will be left over?
A customer is interested in music lessons. The prices listed below are for 10 lessons:
Guitar - £73
Clarinet - £95
Violin - £67
Drums - £92
They decide to buy guitar and violin lessons. How much will it cost in total?
£…………
Price up the following bundles:
 Guitar: £89
Guitar: £89
Amp: £140
Leads: £33
How much will this bundle cost to buy?
£…………

Guitar: £325
Amp: £278
Gig case: £121
How much will this bundle cost to buy?
£…………
The Mega-star bundle costs £989. A customer has a voucher for £299. How much will the bundle cost them now?
£…………

